(...)
A nice way of visualizing the wave/particle duality is the so-called sum over histories introduced by the American scientist Richard Feynman. In this approach the particle is not supposed to have a single history or path in space-time, as it would in a classical, nonquantum theory. Instead it is supposed to go from A to B by every possible path. (Fig. 4.8)
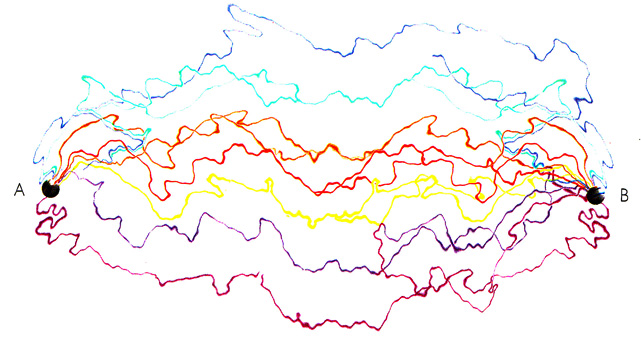 |
Fig. 4.8: In Richard Feynman's theory of sum over histories, a particle in space-time would go from A to B by every possible path.
|
With each path there are associated a couple of numbers: one represents the size of a wave and the other represents the position in the cycle (i.e., whether it is at a crest or a trough). The probability of going from A to B is found by adding up the waves for all the paths. In general, if one compares a set of neighboring paths, the phases or positions in the cycle will differ greatly.This means that the waves associated with these paths will almost exactly cancel each other out. However, for some sets of neighboring paths the phase will not vary much between paths. The waves for these paths will not cancel out. Such paths correspond to Bohr's allowed orbits.
(...)
Einstein's general theory of relativity seems to govern the large-scale structure of the universe. It is what is called a classical theory; that is, it does not take account of the uncertainty principle of quantum mechanics, as it should for consistency with other theories. The reason that this does not lead to any discrepancy with observation is that all the gravitational fields that we normally experience are very weak. However, the singularity theorems discussed earlier indicate that the gravitational field should get very strong in at least two situations, black holes and the big bang. In such strong fields the effects of quantum mechanics should be important. Thus, in a sense, classical general relativity, by predicting points of infinite density, predicts its own downfall, just as classical (that is, nonquantum) mechanics predicted its downfall by suggesting that atoms should collapse to infinite density. We do not yet have a complete consistent theory that unifies general relativity and quantum mechanics, but we do know a number of the features it should have. The consequences that these would have for black holes and the big bang will be described in later chapters. For the moment, however, we shall turn to the recent attempts to bring together our understanding of the other forces of nature into a single, unified quantum theory.
